Research
Machine Learning Potentials
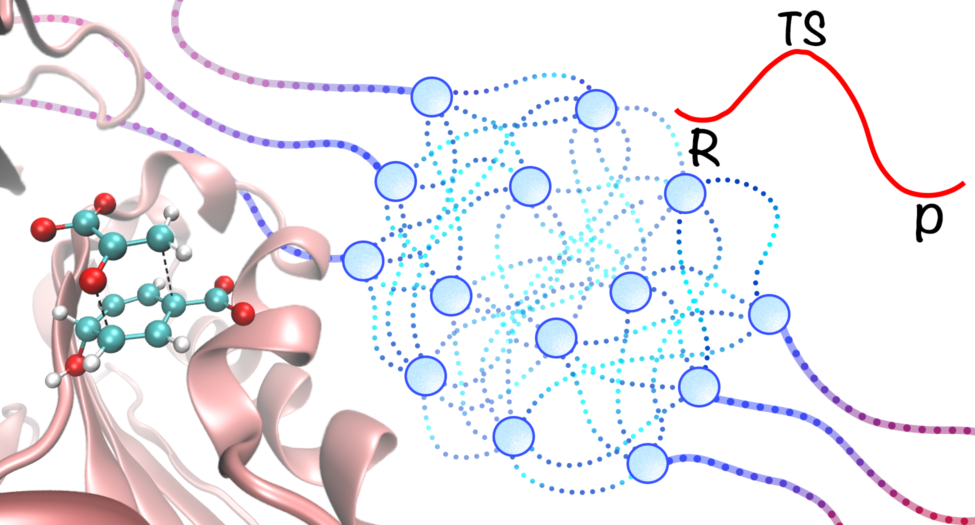
Machine learning potentials (MLPs) are a promising class of empirical potentials that use large datasets generated from high-level quantum mechanical calculations to reproduce the potential energy surface (PES) of a system. These models provide a computationally efficient alternative to expensive quantum mechanical simulations, making them well-suited for simulating complex chemical systems.
By integrating MLPs with multiscale modeling techniques, we have developed an machine learning potential/molecular mechanics (MLP/MM) model that allows for accurate and fast molecular dynamics simulations of chemical processes in complex systems at the quantum mechanical level of accuracy.
Selected Publications
Pan, X.; Yang, J.; Van, R.; Epifanovsky, E.; Ho, J.; Huang, J.; Pu, J.; Mei, Y.; Nam, K.; Shao, Y.; Machine-learning-assisted free energy simulation of solution-phase and enzyme reactions. J. Chem. Theory Comput. 2021, 17, 5745–5758. (Link)
Snyder, R.; Kim, B.; Pan, X.; Shao, Y.; Pu, J.; Facilitating ab initio QM/MM free energy simulations by Gaussian process regression with derivative observations. Phys. Chem. Chem. Phys. 2022, 24, 25134–25143. (Link)
Multiscale Modeling
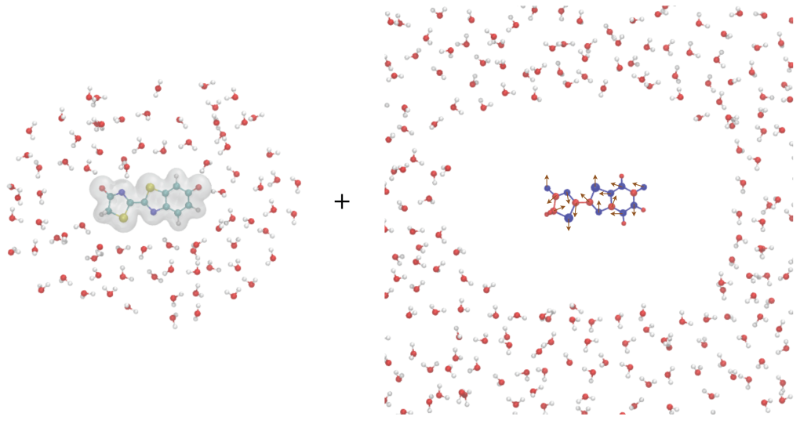
Combined quantum mechanical and molecular mechanical (QM/MM) method is a type of multiscale models that has been widely used in the study of molecular solvation, ligand–receptor binding, chemical/enzyme reactions, and photochemistry. In QM/MM simulations, the system of interest is divided into two regions: the quantum mechanical (QM) region, containing a few hundred atoms that require accurate electronic structure calculations, and the remaining molecular mechanical (MM) region, which can be treated with classical force fields.
For condensed-phase simulations, periodic boundary conditions (PBC) are often necessary to mimic the bulk properties of the system. However, QM/MM calculations under PBC are still challenging due to the lack of efficient long-range electrostatics models and software implementations. To overcome this limitation, we have developed a new QM/MM electrostatics model called the QM/MM augmentary charges (QM/MM-AC) model. This model is specifically designed to be used in PBC simulations and provides accurate electrostatic interactions between the QM and MM regions. The model has been implemented in our QM/MM interface QMHub.
Selected Publications
Pan, X.; Rosta, E.; Shao, Y. Representation of the QM subsystem for long-range electrostatic interaction in non-periodic ab initio QM/MM calculations. Molecules 2018, 23, 2500. (Link)
Pan, X.; Nam, K.; Epifanovsky, E.; Simmonett, A. C.; Rosta, E.; Shao, Y.; A simplified charge projection scheme for long-range electrostatics in ab initio QM/MM calculations. J. Chem. Phys. 2021, 154, 024115. (Link)
Enhanced Sampling and Free Energy Calculations
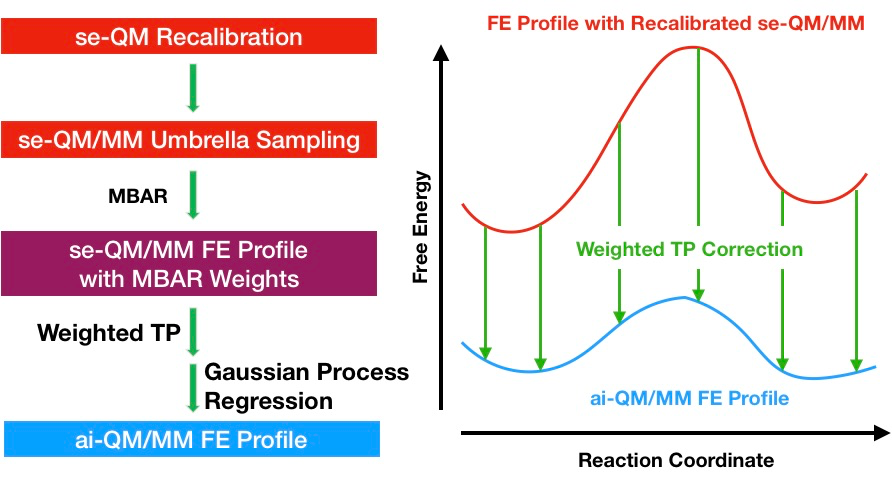
Free energy calculations can provide detailed insights into chemical processes, but they can be prohibitively expensive, especially when using ab initio quantum mechanical methods. To address this challenge, we have developed two methods based on the dual Hamiltonian strategy to accelerate these calculations.
The first method is the reference-potential method where the sampling is done at the low level of theory and the free energy at a high level of theory is calculated using the weighted thermodynamic perturbation method. The reference potential can be a semi-empirical potential or a force field potential.
The second method is the multiple time step (MTS) method, which involves doing high-level force calculations only at the outer steps of the MTS integrator, while low-level forces are calculated at the inner steps. This reduces the computational cost significantly while maintaining high accuracy.
Selected Publications
Pan, X.; Li, P.; Ho, J.; Pu, J.; Mei, Y.; Shao, Y.; Accelerated computation of free energy profile at ab initio quantum mechanical/molecular mechanics accuracy via a semi-empirical reference potential. II. Recalibrating semi-empirical parameters with force matching. Phys. Chem. Chem. Phys. 2019, 21, 20595–20605. (Link)
Pan, X.; Van, R.; Epifanovsky, E.; Liu, J.; Pu, J.; Nam, K.; Shao, Y.; Accelerating ab initio quantum mechanical and molecular mechanical (QM/MM) molecular dynamics simulations with multiple time step integration and a recalibrated semiempirical QM/MM Hamiltonian. J. Phys. Chem. B 2022, 126, 4226–4235. (Link)
Enzyme Catalysis
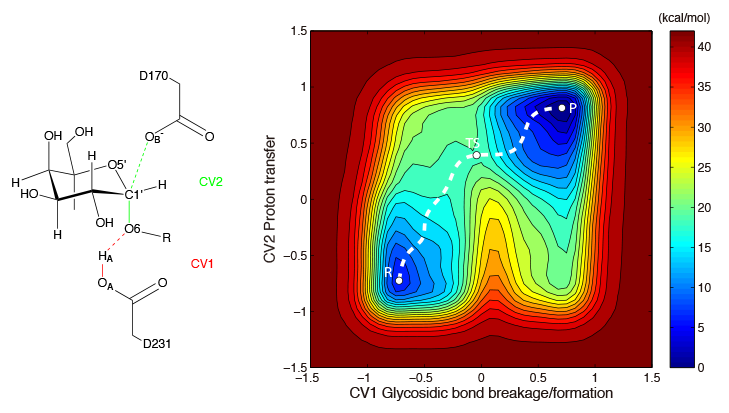
Enzymes are biological catalysts that facilitate chemical reactions within living organisms. Computational methods, such as QM/MM free energy calculations, are often used to study the catalytic mechanism of enzymes. Understanding the mechanisms by which enzymes catalyze reactions is essential not only for gaining insight into the biological function of enzymes, but also for designing more efficient enzymes for use in biotechnological applications. By comprehending how enzymes work at the molecular level, we can manipulate and optimize their activity to produce new and improved catalysts that can be used in a variety of fields, from medicine to energy production.
Selected Publications
Pan, X.; Liu, W.; Liu, J. Mechanism of the glycosylation step catalyzed by human α-galactosidase: A QM/MM metadynamics study. J. Phys. Chem. B 2013, 117, 484–489. (Link)
Pan, X.; Schwartz, S. D. Conformational heterogeneity in the Michaelis complex of lactate dehydrogenase: An analysis of vibrational spectroscopy using Markov and hidden Markov models. J. Phys. Chem. B 2016, 120, 6612–6620. (Link)